Της Ισμύνης Παπαγιαννοπούλου,
Η Ελλάδα έχει ισχυρή παρουσία στον τομέα των θετικών επιστημών λόγω του ότι είναι η γενέτειρα των δυτικών μαθηματικών και της γεωμετρίας. Θαλής, Πυθαγόρας, Αρχιμήδης, Δημόκριτος, Ευκλείδης, Απολλώνιος ο Περγαίος είναι μερικοί μόνον από τους παγκοσμίως γνωστούς μαθηματικούς που έδωσαν τις βάσεις για την εξέλιξη της γεωμετρίας, της αστρονομίας, των μαθηματικών κ.ο.κ. Επομένως, δεν θα έπρεπε να αποτελεί έκπληξη ότι έχουν αναπτυχθεί θεωρίες που υποστηρίζουν ότι οι αρχαίες ελληνικές τοποθεσίες μπορεί να είχαν κατασκευαστεί σύμφωνα με ένα «κύριο σχέδιο». Αν και αυτές οι θεωρίες σίγουρα δεν είναι ”mainstream” και μερικά από τα πιο ακραία παραδείγματα απαιτούν μεγάλα άλματα φαντασίας, υπάρχουν μερικά ενδιαφέροντα παραδείγματα επιστημονικά αποδεδειγμένα. Ένα από αυτά αναφέρεται ως το Ιερό Τρίγωνο ή Τρίγωνα.
Η γεωδαισία είναι η επιστήμη που ασχολείται με την ακριβή περιγραφή της γήινης επιφάνειας. Οι αρχαίοι τη γνώριζαν καλά και την ώρα που για κάποιους άλλους ήταν μια σπαζοκεφαλιά, εκείνοι απλώς την έπαιζαν στα δάχτυλα. Τόσο ο Πλάτων στην Πολιτεία όσο και ο Στράβων παραδέχονται ότι η ίδρυση των ιερών ναών δεν γινόταν συμπωματικά, αλλά ακολουθούσε έναν εσωτερικό κανονισμό με τη δική του απόκρυφη μεθοδολογία, αν και αμφότεροι εμφανίζονται διστακτικοί να αποκαλύψουν τις λεπτομέρειες της θείας αυτής αναλογίας. Ήταν κοινή σε όλους γνώση και δεν χρειαζόταν περισσότερη ανάλυση; Ή μήπως επρόκειτο για απόκρυφες ιερατικές διδασκαλίες που μόνο οι μυημένοι έπρεπε να κατέχουν;
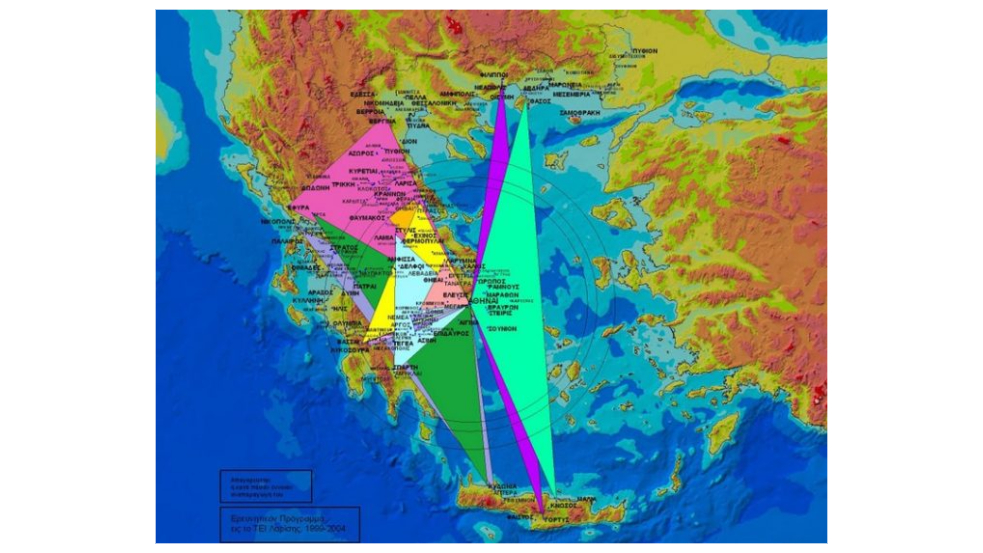
Εάν κοιτάξει κανείς τον χάρτη και εντοπίσει τις τοποθεσίες των αρχαίων ναών, θα δει ότι σχηματίζουν ισόπλευρα και ισοσκελή τρίγωνα. Χαρακτηριστικό και πιο δημοφιλές παράδειγμα αποτελεί η πρώτη τριπλέτα με τον Ναό του Ποσειδώνα στο Σούνιο, τον Ναό της Αφαίας Αθηνάς στην Αίγινα και τον Ναό του Ηφαίστου στο Θησείο της Αθήνας, που σχηματίζουν ένα ισοσκελές τρίγωνο. Ένα άλλο είναι αυτό του Ναού του Απόλλωνα στους Δελφούς, του Παρθενώνα και του Ναού της Αφαίας στην Αίγινα. Ακόμη πιο ενδιαφέρον είναι ότι και οι τρεις ναοί χτίστηκαν μέσα σε λίγα χρόνια ο ένας από τον άλλο, προσθέτοντας στη θεωρία ότι η τοποθέτησή τους ήταν μέρος ενός μεγαλύτερου σχεδίου. Η συμμετρία υφίσταται, ωστόσο υπάρχουν διάφορες θεωρίες για το ποιον σκοπό εξυπηρετεί. Οι πρώτες πρωινές ακτίνες του ήλιου την ημέρα του εορτασμού του θεού στον οποίο ήταν αφιερωμένος ο κάθε ναός, έπρεπε να διαπερνούν τον κεντρικό άξονά του, φωτίζοντας το κεντρικό άγαλμα του θεού. Οι υπολογισμοί, όπως άρχισαν να αποδεικνύουν πια, από τα τέλη της δεκαετίας του ’60 και μετά με τα εξελιγμένα μέσα υπολογισμών, ήταν ολόσωστοι. Ούτε η παρεμβολή της θάλασσας στάθηκε ποτέ εμπόδιο στην ακρίβειά τους, ούτε κανένας άλλος παράγοντας.
Η αφετηρία της ανακάλυψης
Παρά το γεγονός ότι σε αρχαία κείμενα συναντούμε διάσπαρτες αναφορές για τον γεωμετρικό τριγωνισμό και η ύπαρξη των αρμονικών αυτών σχέσεων δεν ήταν κατά κανέναν τρόπο μυστική, η αρμονία και το κάλλος της νοητής διασύνδεσης των αρχαιοελληνικών ιερών μπήκε στο στόχαστρο του Γάλλου ερευνητή Ζαν Ρισσέν το 1967, ο οποίος έκανε ρητή αναφορά στον «Αρχαίο Γεωμετρικό Τριγωνισμό» και προσπάθησε να διαπιστώσει στην πράξη αν πράγματι οι αρχαίοι ήταν ειδήμονες σε μαθηματικά παιχνίδια πάνω στον χάρτη.
Tο γάντι της πρόκλησης αυτής σήκωσε, στη συνέχεια, ο Θεοφάνης Μανιάς («Άγνωστα Μεγαλουργήματα των Αρχαίων Ελλήνων») και αργότερα ο Α. Αλεξίου, οι οποίοι από τις αρχές της δεκαετίας του 1970 άρχισαν να μελετούν την εσωτερική μαθηματική και αστρονομική αρμονία των αρχαιοελληνικών μνημείων. Οι εκατοντάδες επιτόπιες θεσιακές μετρήσεις σε ναούς και ιερά της Ελλάδας του καθηγητή Κοσμά Μαρκάτου, ο οποίος συνέχισε την δική του έρευνα, αποκάλυψαν ότι το ισοσκελές τρίγωνο ήταν πιθανότατα η μονάδα του γεωδαιτικού τριγωνισμού, αν και έχουν χρησιμοποιηθεί κι άλλα πρότυπα, όπως η αρχή των ίσων αποστάσεων μεταξύ των αρχαιολογικών χώρων, το ορθογώνιο, το ισόπλευρο και το χρυσό τρίγωνο, ο κύκλος, ο ευθυγραμμισμός κ.ά. Με τη βοήθεια του GPS ο ισοσκελισμός των πλευρών των ιερών αυτών τριγώνων έφτανε σχεδόν την τελειότητα, καθώς οι αποκλίσεις κυμαίνονταν από μερικά εκατοστά έως μέχρι μερικές δεκάδες και μόνον μέτρα. Το πιο αδιανόητο είναι ότι κάθε φορά που οι Μεγάλοι Γεωμέτρες της αρχαιότητας δημιουργούν στον χάρτη της Αττικής ένα νέο ισοσκελές τρίγωνο, αφετηρία τους είναι ένας από τους ναούς του αμέσως προηγούμενου ισοσκελούς τριγώνου!
Οι 5 πιο γνωστές τριπλέτες:
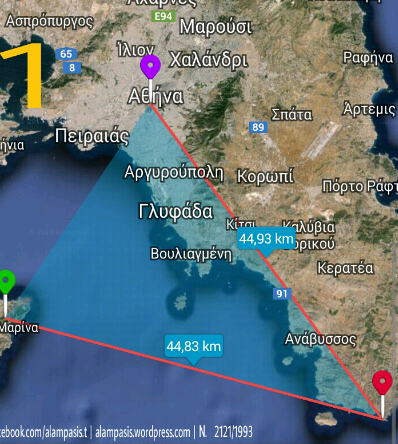
- Ναός του Ποσειδώνα στο Σούνιο – ναός της Αφαίας στην Αίγινα – ναός του Ηφαίστου στο Θησείο. Έχει πλευρές μήκους 44,83 χιλιόμετρα (Ναός του Ποσειδώνα, Σούνιο – Ναός της Αφαίας, Αίγινα) και 44,93 χιλιόμετρα (Ναός του Ποσειδώνα, Σούνιο – Ναός του Ηφαίστου, Θησείο). Η περίμετρος του τριγώνου είναι 89,763 χιλιόμετρα και το εμβαδό του 628,52 τετραγωνικά χιλιόμετρα.
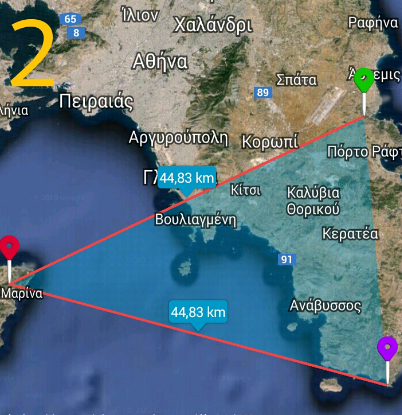
- Από το προηγούμενο τρίγωνο κρατάνε τον Ναό του Ποσειδώνα στο Σούνιο και δημιουργούν το επόμενο. Πρόκειται για το ισοσκελές τρίγωνο με κορυφή τον ναό της Αφαίας στην Αίγινα και πλευρές α) τον Ναό του Ποσειδώνα στο Σούνιο και β) τον ναό της Αρτέμιδος στη Βραυρώνα. Το ισοσκελές τρίγωνο έχει πλευρές μήκους 44,83 χιλιόμετρα (Ναός του Ποσειδώνα, Σούνιο – Ναός της Αφαίας, Αίγινα) και 44,83 χιλιόμετρα (Ναός της Αφαίας, Αίγινα – Ναός της Αρτέμιδος, Βραυρώνα). Η περίμετρος του τριγώνου είναι 89,657 χιλιόμετρα.
- Από το προηγούμενο τρίγωνο κρατάνε τον Ναό της Αρτέμιδος στη Βραυρώνα και δημιουργούν το επόμενο. Πρόκειται για το τρίγωνο με κορυφή τον Ναό της Αρτέμιδος στη Βραυρώνα και πλευρές α) τον ναό της Δήμητρος στην Ελευσίνα και β) τον ναό του Αμφιάραου (στον Ωρωπό Αττικής) που υπήρξε ιερός χώρος και μαντείο αφιερωμένο στον μυθικό ήρωα Αμφιάραο. Το ισοσκελές τρίγωνο έχει πλευρές μήκους 42,21 χιλιόμετρα (Ναός της Αρτέμιδος, Βραυρώνα – Ιερό της Δήμητρος, Ελευσίνα) και 42,62 χιλιόμετρα (ναός της Αρτέμιδος, Βραυρώνα – Ναός του Αμφιαράου, Ωρωπός). Το εμβαδόν του τριγώνου είναι 731,34 τετραγωνικά χιλιόμετρα
- Από το προηγούμενο τρίγωνο κρατάνε τον Ναό του Αμφιαράου στον Ωρωπό και δημιουργούν το επόμενο. Πρόκειται για το τρίγωνο με κορυφή τον ναό του Ολυμπίου Διός στο Ζάππειο και πλευρές α) τον Ναό του Αμφιαράου στον Ωρωπό και β) το αρχαίο θέατρο στα ερείπια του οικισμού του αρχαίου Θορικού. Το ισοσκελές τρίγωνο έχει πλευρές μήκους 37,41 χιλιόμετρα (Στήλες Ολυμπίου Διός, Ζάππειο – Ναός του Αμφιαράου, Ωρωπός) και 37,64 χιλιόμετρα (Στήλες Ολυμπίου Διός, Ζάππειο – αρχαίο θέατρο Θορικού). Το εμβαδόν του τριγώνου είναι 627,14 τετραγωνικά χιλιόμετρα.
- Από το προηγούμενο τρίγωνο κρατάνε το Αρχαίο Θέατρο στο Θορικό και δημιουργούν το επόμενο. Πρόκειται για το τρίγωνο με κορυφή τον Παρθενώνα στην Ακρόπολη και πλευρές α) το Αρχαίο Θέατρο στο Θορικό και β) το ναό της Νεμέσεως στον Ραμνούντα στον Μαραθώνα. Το ισοσκελές τρίγωνο έχει πλευρές μήκους 38,4 χιλιόμετρα (Παρθενώνας – Αρχαίο θέατρο Θορικού) και 38,07 χιλιόμετρα (Παρθενώνας – ναός της Νεμέσεως στον Ραμνούντα). Το εμβαδόν του τριγώνου είναι 730,49 τετραγωνικά χιλιόμετρα.
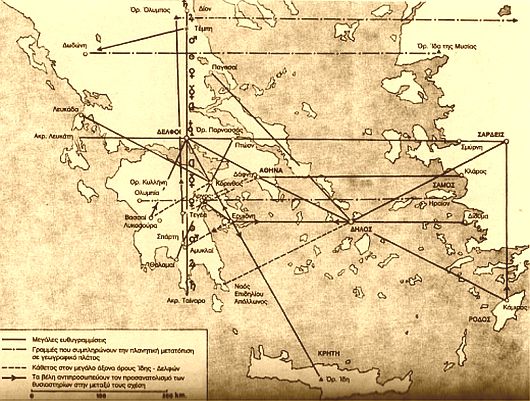
Οι τριγωνομετρικές σχέσεις που σχηματίζουν μεταξύ τους οι Ιεροί Τόποι των Ελλήνων είναι χαρακτηριστικές. Το μαντείο της Δωδώνης βρίσκεται ευθυγραμμισμένο με το μαντείο των Δελφών, την Ακρόπολη των Αθηνών και τη Δήλο, ενώ, παράλληλα, ισαπέχει από Αθήνα – Σπάρτη (1.700 στάδια), Δελφούς – Ιωλκό (1.050 στάδια), Ολυμπία – Τροφώνιο Μαντείο (1.240 στάδια), Ανάκτορα Νέστορα – Ελευσίνα (1600 στάδια), Κνωσσό – Μίλητο (3.300 στάδια).
Το ισοσκελές τρίγωνο που ορίζουν οι περιοχές Δωδώνη – Ανάκτορα Νέστορα – Ελευσίνα, με γωνία κορυφής 40°, ανήκει σε κανονικό εννιάγωνο. Το ισοσκελές τρίγωνο Δωδώνης – Ολυμπίας – Τροφωνίου Μαντείου ανήκει σε κανονικό δεκάγωνο, τα γεωμετρικά στοιχεία του οποίου προεκτεινόμενα συναντούν πόλεις όπως το Ίλιον (Τροία), Σμύρνη, Κνωσσός, Φαιστός, Σπάρτη κ.α. Το τρίγωνο Δωδώνης – Κνωσσού – Μιλήτου ανήκει σε κανονικό δωδεκάγωνο με γωνία κορυφής 30°. Το τρίγωνο Δωδώνης – Δελφών – Ιωλκού είναι ισοσκελές και ανήκει σε κανονικό δωδεκάγωνο. Το τρίγωνο Δωδώνης – Αθήνας – Σπάρτης ανήκει σε κανονικό πολύγωνο με δεκατρείς πλευρές.
Το γιατί έχτιζαν οι αρχαίοι Έλληνες τους χώρους λατρείας τους κατά τρόπο που να δημιουργούν στον χάρτη ισόπλευρα και ισοσκελή τρίγωνα ή να επαληθεύουν περίπλοκες μαθηματικές σχέσεις παραμένει το μεγάλο ζητούμενο, με τα ερωτήματα που ανακύπτουν να είναι πολλά και ποικίλα από πολλούς ερευνητές παγκοσμίως. Ίσως κάποιος υποθέσει ότι πρόκειται για απλές συμπτώσεις και ότι είναι φυσικό να υπάρχουν τέτοιοι συσχετισμοί, εφόσον στην αρχαιότητα υπήρχαν πάρα πολλοί ιεροί τόποι και άλλα μέρη ιδιαίτερης σημασίας στον ελληνικό χώρο. Πιθανόν, μάλιστα, να θεωρηθεί υπερβολικό το ότι οι ερευνητές έχουν διαπιστώσει την αναλογική συσχέτιση τόσο πολλών κωδικών σημείων μεταξύ τους! Όμως αυτόματα έρχεται η απάντηση από τον Ήρωνα τον Αλεξανδρέα: «Ἡ γεωδαισία ποιεῖται τὰς διαιρέσεις οὐ μόνον εἰς ἰσότητας ἀλλὰ καὶ κατὰ λόγους καὶ ἀναλογίας». Τι εξυπηρετούσε η ιερή αυτή χωροθεσία, αλλά και πώς υπολόγιζαν τις τεράστιες αποστάσεις, πολλώ δε μάλλον όταν παρεμβαλλόταν ανάμεσά τους η θάλασσα; Ήταν μια προσπάθεια αναπαράστασης πάνω στη γη των περίλαμπρων αστερισμών του ουρανού; Ή ήθελαν αντιθέτως να απεικονίσουν στον ελλαδικό χάρτη όλο τον ζωδιακό κύκλο, κάνοντας το Κοινό των Ελλήνων την τέλεια αντανάκλαση της προαιώνιας ουράνιας αρμονίας πάνω στη γη; Ή μήπως έκαναν χρήση των γεωενεργειακών ρευστών, των φυσικών ενεργειακών ρευμάτων της γήινης επιφάνειας, δηλαδή κατευθύνοντας την ενέργεια στις πόλεις και τα ιερά τους;
Πέρα από τα φυσικά και μεταφυσικά «γιατί», είναι αυτό το ακανθώδες «πώς» που οφείλει να εντυπωσιάσει επιτέλους τη μοντέρνα σκέψη: πώς κατάφεραν, δηλαδή, οι αρχαίοι Έλληνες τον τιτάνιο άθλο της γεωμετρικής διασύνδεσης των ιερών τους τόπων; Μια πειστική απάντηση εδώ θα φωτίσει σαφώς διαφορετικά όλα όσα ξέρουμε για την επιστημοσύνη, αλλά και τη μυστικιστική γνώση ενός από τους λαμπρότερους πολιτισμούς που εμφανίστηκαν ποτέ στον πλανήτη Γη.
ΕΝΔΕΙΚΤΙΚΗ ΒΙΒΛΙΟΓΡΑΦΙΑ
- The Sacred Triangle of Greece – Myth or Fact?, greekmythologytours.com, Διαθέσιμο εδώ
- Ιερή Γεωδαισία των Αρχαίων Ελλήνων – Τα 5 ισοσκελή τρίγωνα της Αττικής, kokkinoslawfirm.com, Διαθέσιμο εδώ
- Αρχαία Ελλάδα: Τα ιερά τρίγωνα και η καλά κρυμμένη σημασία τους, upsite.gr, Διαθέσιμο εδώ
- Thales: Ancient Greeks built the cosmos with right triangles, bigthink.com, Διαθέσιμο εδώ
- Richer, J. (2001), Ἡ Ἱερὴ Γεωγραφία τοῦ Ἑλληνικοῦ Κόσμου, ἐκδ. Κυβέλη.